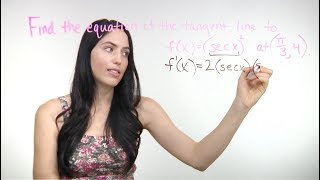Деривативы... Что? (НэнсиПи)

Выпускник Массачусетского технологического института показывает ОПРЕДЕЛЕНИЕ производной и как НАЙТИ производную, используя это предельное определение. Чтобы перейти дальше: 1) Что означает производная, перейдите к 0:23. 2) Что касается НАКЛОНА СЕКУЩЕЙ, перейдите к 2:53. 3) Что касается ПРЕВРАЩЕНИЯ СЕКУЩЕЙ В ТАНГЕНЦИЮ и ОПРЕДЕЛЕНИЯ ПРОИЗВОДНОЙ, перейдите к 5:54. 4) Как НАЙТИ ПРОИЗВОДНУЮ, ИСПОЛЬЗУЯ (ПРЕДЕЛ) ОПРЕДЕЛЕНИЯ производной, перейдите к 10:28. Нэнси, ранее работавшая в MathBFF, объясняет шаги. Чтобы посмотреть моё видео о более коротких и быстрых ПРАВИЛАХ ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ, перейдите по ссылке:    • Derivatives... How? (NancyPi)   Подпишитесь на Нэнси в Instagram:   / nancypi   Твиттер:   / nancypi   ВВЕДЕНИЕ в производные: 1) ЧТО ТАКОЕ ПРОИЗВОДНАЯ? Это функция, которая определяет наклон (касательной к кривой) в каждой точке. Другими словами, производная показывает скорость изменения в любой момент времени («мгновенную скорость изменения» в каждой точке). Вы можете найти производную либо с помощью правильного ОПРЕДЕЛЕНИЯ ПРОИЗВОДНОЙ («по предельному методу»), либо более быстрым и простым способом, используя упрощённые правила вычисления производной, такие как правило степенной функции, правило произведения, правило частного и цепное правило. В этом видео показан первый способ, а также ОПРЕДЕЛЕНИЕ производной и как использовать его для вычисления производной. 2) НАКЛОН СЕКУЩЕЙ: Чтобы определить производную, мы можем начать с наклона прямой, проходящей через точку x и другую точку, расположенную рядом, на расстоянии h по горизонтали. Если мы обозначим две точки и воспользуемся формулой наклона, чтобы записать выражение для наклона этой секущей, то получим выражение [f(x+h) - f(x)] / h, которое также известно как РАЗНОСТНОЕ ЧАСТНОЕ. 3) ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ: Наклон прямой, который мы только что нашли, на самом деле является точной ОЦЕНКОЙ наклона в точке x, но на самом деле это не наклон в точке x. Мы можем получить ТОЧНЫЙ наклон касательной в точке x, приближаясь к x и сужая h до нуля, взяв ПРЕДЕЛ наклона секущей, когда h стремится к 0. Наклон секущей становится наклоном касательной. Этот предел не только равен наклону касательной, но и является определением производной (если предел существует) или f'(x). 4) КАК НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ, ИСПОЛЬЗУЯ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА: Если вам нужно найти производную «используя определение производной» или «с помощью предельного процесса», то вы можете использовать определение предела, которое мы только что нашли для любого данного уравнения f(x). Помните, что часть формулы f(x+h) означает замену x на (x+h) в любом месте x, где x встречается в функции f(x). Если вам нужна помощь в нахождении предела в конце, посмотрите моё видео «Как найти любой предел»:    • How to Find Any Limit (NancyPi)   Чтобы познакомиться с концепцией пределов, перейдите по ссылке:    • Introduction to Limits (NancyPi)   Другие мои видео по математике, математическому анализу, предвычислениям и алгебре можно найти здесь: http://nancypi.com