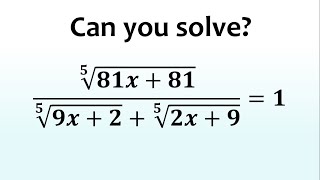Можете ли вы решить это алгебраическое уравнение ЛЕГКИМ способом?

Испытываете трудности с алгебраическими уравнениями? В этом уроке по математике мы решим уравнение ((x+1)/(x-2))² + ((x+1)/(x-3)) = 12((x-2)/(x-3))², используя элегантный метод подстановки, который позволяет избежать утомительного вычисления. Вместо того, чтобы преобразовывать уравнение в сложную четвертую степень, мы упрощаем его до A² + AB = 12B², а затем разлагаем на множители, чтобы получить два более простых соотношения: A = 3B и A = -4B. Этот подход показывает, как подстановка и алгебраические рассуждения могут превратить, казалось бы, сложное уравнение в простое решение. Идеально подходит для старшеклассников, учащихся старших классов и участников математических олимпиад, желающих улучшить свои навыки алгебры и методы решения задач. 00:00 Введение — нахождение действительных значений x в рациональном уравнении 00:10 Подстановка: пусть A = (x+1)/(x−2) и B = (x−2)/(x−3) 00:34 Переписываем исходное уравнение через a и b 00:46 Упрощаем, чтобы получить A² + AB = 12B² 01:18 Составление и преобразование квадратного уравнения относительно a и b 01:36 Пошаговое объяснение факторизации табличным методом 02:18 Получение двух уравнений: A = 3B и A = −4B 03:20 Подстановка A и B обратно через x 04:09 Первое уравнение: решение (x+1)/(x−2) = 3(x−2)/(x−3) 04:30 Перекрёстное умножение и разложение Скобки 05:43 Упрощение и преобразование в квадратное уравнение 06:35 Проверка на наличие действительных корней методом дискриминанта 07:31 Объяснение, почему у этого квадратного уравнения нет действительных корней 07:59 Второе уравнение: решение (x+1)/(x−2) = −4(x−2)/(x−3) 08:24 Пошаговое описание перекрёстного умножения и полного разложения 09:15 Упрощение и преобразование для получения 5x² − 8x + 13 = 0 10:22 Разложение квадратного уравнения табличным методом 11:23 Нахождение возможных значений x для каждого множителя 11:58 Окончательные действительные решения: x = 1 и x = 13/5 12:14 Заключение и призыв подписаться на новые уроки по математике Не забудьте поставить лайк 👍 и подписаться https://www.youtube.com/@NonsoMaths?s...
и нажмите на колокольчик, чтобы получать больше математических советов и подсказок! #матолимпиада #урок по математике #алгебра